A very rare and wonderful book came into my hands via John Martineau. I've scanned it below so it may live on for many more years! Thanks to Mrs Watts Hughes who authored this pioneering text. Apologies for the scanning not ...Read More
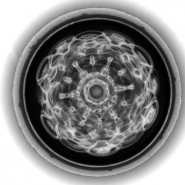
This is a track called 'Wah' sent to me by didgeridoo player Ken Shapley.
I visualised it using my cymatics water setup.
To give you physical scale this is about 3cm across.
The only post production I've done is to mask around it ...Read More

Each frame of this video is a photograph taken from a specific frequency played in water. Read More

John explains and demonstrates cymatics using harmonicism and a range of custom built instruments. Read More

90% Water is a sculptural installation which uses water, sound and silence to create a hypnotic, ever changing pool for reflection, contemplation and intrigue. I created a 20min track which plays on a loop. The track consists of sounds and ...Read More

This audio-visual scientific art project - founded by Jan Zehn in 1999 - focusses on the development of creative art tools and instruments for cymatics based spatial image and sound design and animation.
Understanding Cymatics as the basical process of creating ...Read More

Using computer visualization software, Mark Fischer transforms mysterious underwater calls of cetaceans (whales and dolphins) into "wavelets": visual readings of the sounds' volume, harmonics, frequencies and rhythms. The result are stunning ripples of printed color or animated soundscapes, revealing the ...Read More






